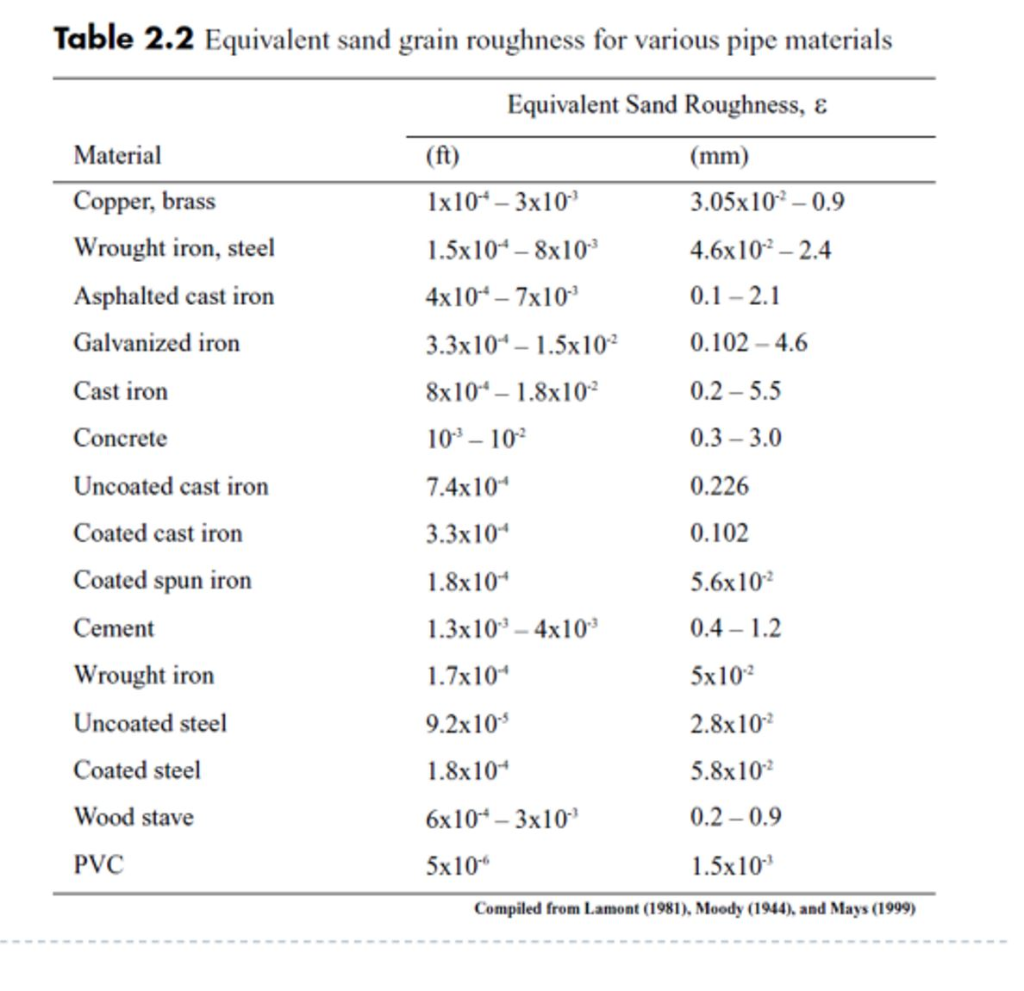
Pipe Roughness There are different systems for calculating the pipe roughness, but typically, the higher the value, the rougher the pipe, and the more losses due to friction. Based on the chart above, drawn brass or copper will be the smoothest and most efficient option, while concrete would be the roughest and least efficient option. Absolute Pipe Roughness: Included here is a sampling of absolute pipe roughness e data taken from Binder (1973). These values are for new pipes; aged pipes typically exhibit in rise in apparent roughness. In some cases this rise can be very significant. Material: Nature of Material: Roughness mm Roughness inch Steel pipe: drawn, new: 0.02 - 0.1: 0.0008 - 0.004: welded, new: 0.05 - 0.1: 0.002 - 0.004.
- Relative Roughness Of Copper Nickel Pipe
- Equivalent Roughness Of Copper Pipe
- Equivalent Roughness Of Copper Pipe
- Roughness Of Pvc Pipe
Pressure losses distributed in the pipes |
Absolute Roughness Coefficient - k - (10-3 m) (feet) Drawn Copper, Lead, Brass, Aluminum (new) and the like: 0.001 - 0.002 (3.28 - 6.56) 10-6: PVC, PE and other smooth Plastic Pipes: 0.0015 - 0.007 (0.49 - 2.30) 10-5: Stainless steel, bead blasted: 0.001 - 0.006 (0.00328 - 0.0197) 10-3: Stainless steel, turned: 0.0004 - 0.006 (0.00131 - 0.0197) 10-3. Copper, brass, lead, tin or glass pipe or tubing 150/120 140 130 Wood Stave 145/110 120 110 Welded or Seamless Steel 150/80 130 100 Cast and ductile iron 150/80 130 100 Concrete 152/85 120 100 Corrugated steel - 60 60 Manning’s Equation roughness coefficient (n) Material Values for n Range Typical Design Value Polyethylene pipe 0.008-0.011 0.
The calculation of the linear pressure loss, that corresponding to the general flow in a rectilinear conduit, is given by the following general formula:

- Dp= pressure loss in Pa
- L=friction factor (a number without dimension)
- p =density of water in kg/m3
- V=flow rate in m/s
- D=pipe diameter in m
- L=pipe length in m
The expression above shows that calculations of pressure losses rest entirely on the determination of the coefficient L.
| Flow type |
The nature of the type of flow of a fluid is determined by the value of the Reynolds number.
The various types of flows are visualized by the chart of the diagram of Moody using the Reynolds number for the x axis and the factor of friction F for the y axis.
The mode of flow of a fluid is characterized in 3 forms:
| Laminar mode | Reynolds number lower than 2000 indicates than the flow is calm and regular |
| Turbulent mode | Reynolds number higher than 4000 indicates than the flow is in the form of swirl and of movement. |
| Zone critique | Reynolds number located 2000 and 4000 indicates that the flow is unstable between the laminar mode and the turbulent mode. |

| Calculation of the Reynolds number |
The Reynolds number is no dimensional (thus without units). It combines 3 significant characteristics of the flow and the fluid: speed, density and viscosity. The diameter is necessary to make the number no dimensional. One calls the diameter the characteristic length. A Reynolds number of 2000 or less indicates a flow in laminar mode while a number of 4000 where more a turbulent flow indicates.
The Reynolds number is defined is:
According to kinematics viscosity | According to dynamics viscosity |
(legal System (S.I) in m²/s = 1000000 centistokes or mm²/s) |
|
Reynolds number is inversely proportional to kinematics viscosity.
The viscosity of a fluid is a characteristic which makes it possible to determine resistance to the movement of the fluid. The higher kinematic viscosity will be and the more difficult it will be to move the fluid in the pipe.
Kinematics viscosity (v is the ratio of dynamic viscosity on the density of the fluid.
Kinematics viscosity in m2/s | kinematics viscosity in mm²/s (or centistokes) |
| |
| Loss pressure |
Laminar flow (Re £ 2000)
In rate of laminar, the nature or the surface quality of the interior walls of the lines does not intervene in the calculation of the pressure loss.
The loss pressure is determined by the following function:

- L=friction factor (a number without dimension)
- Re=Reynolds number
The laminar flow meets in practice only in the transport and the handling of the viscous fluids, such as the crude oil, fuel oil, oils, etc.
Turbulent flow (Re > 2000)
Relative Roughness Of Copper Nickel Pipe
In the critical zone, i.e. between 2000 and 4000 Reynolds the formula of computation employed will be treated in the manner that in situation of mode of turbulent flow.
In rate of turbulent, the factor of friction is translated by the formula of Colebrook considered as that which translates best the phenomena of flow into turbulent mode.
It is noted that this formula is in implicit form; consequently search can be done only by successive approaches (iterative calculation)
With:
Equivalent Roughness Of Copper Pipe
- L=friction factor (a number without dimension)
- D =pressure loss coefficient.
- k=index of roughness of the pipe.
- d=pipe diameter in mm.
- Re=Reynolds number.
Usual value index of roughness (k) in mm | ||||
Nature of interior surface | Index roughness K | |||
1 | Copper, lead, brass, stainless | 0,001 to 0,002 | ||
2 | PVC pipe | 0,0015 | ||
3 | Stainless steel | 0,015 | ||
4 | Steel commercial pipe | 0,045 à 0,09 | ||
5 | Stretched steel | 0,015 | ||
6 | Weld steel | 0,045 | ||
7 | Galvanized steel | 0,15 | ||
8 | Rusted steel | 0,1 to 1 | ||
9 | New cast iron | 0,25 to 0,8 | ||
10 | Worn cast iron | 0,8 to 1,5 | ||
11 | Rusty cast iron | 1,5 to 2,5 | ||
12 | Sheet or asphalted cast iron | 0,01 to 0,015 | ||
13 | Smoothed cement | 0,3 | ||
14 | Ordinary concrete | 1 | ||
15 | Coarse concrete | 5 | ||
16 | Well planed wood | 5 | ||
17 | Ordinary wood | 1 | ||
| Influence rate of antifreeze (glycol) |
In the case of an addition of antifreeze (glycol) to water, kinematics viscosity (into centistokes) varies in the following way:
Equivalent Roughness Of Copper Pipe
- t = temperature at 0°C
- a = percentage of glycol
Roughness Of Pvc Pipe
Last update: